PageRank - Dead Ends & Spider Traps

해당 포스팅은 스탠포드의 Jure Leskovec 교수님의 강의 와 Mining of Massive Datasets(Jure Leskovec, Anand Rajaraman, Jeff Ullman) 책 을 참고하였습니다.

지난 포스팅에서는

기존 웹 구조에 iteration 방식을 사용하여 importance 를 구하는 경우

발생하는 문제 상황에 대해 언급하였습니다.

이번 포스팅에서는 문제 상황과 이를 해결하는 방식에 대해 다룹니다.

Avoiding Dead Ends

노드, 페이지의 아웃링크가 없는 것을 데드엔드(Dead Ends)라 합니다.

만약 데드엔드르 허용된다면 웹의 변환 행렬 M은 더이상 확률적(Stochatic)이지 않습니다. 이 경우 특정 칼럼의 합이 1이 아니라 0이 될 수 있습니다.

열의 합이 최대 1 인 행렬을 substochastic 라고 하는데, 이 substochastic 행렬 M 으로 $M^iv$ 를 계산하면, 벡터의 일부 혹은 전체가 0이 됩니다.

이것을 웹에서는 Importance drain out 이라고 하고,

이 상황에서는 페이지의 상대 중요도에 대한 정보를 얻을 수 없게 됩니다.

데드엔드를 다루는 2가지 방법이 있습니다.

데드엔드 노드와 데드엔드로 가는 엣지를 그래프에서 빼고 처리합니다. 이렇게 하면 더 많은 데드엔드가 생성될 수도 있습니다. 기존 데드엔드로 향하는 out link 만 갖고 있는 노드는 삭제 작업 후에 데드엔드가 됩니다. 그러나, 이 삭제 작업을 반복(recursive)하다보면 SCC를 얻게 됩니다. (SCC 는 데드엔드가 없습니다.)

이렇게 얻은 SCC 그래프 G 는 이후 나올 taxation 이나 기존 방식을 사용하여 페이지 랭크를 구할 수 있습니다.

G의 노드에 대한 페이지랭크 값을 먼저 구한후, 기존 그래프를 복구합니다.

G에 있지 않지만 기존 그래프에 있던 노드의 페이지 랭크는 G의 페이지 랭크 값을 통해 구합니다.

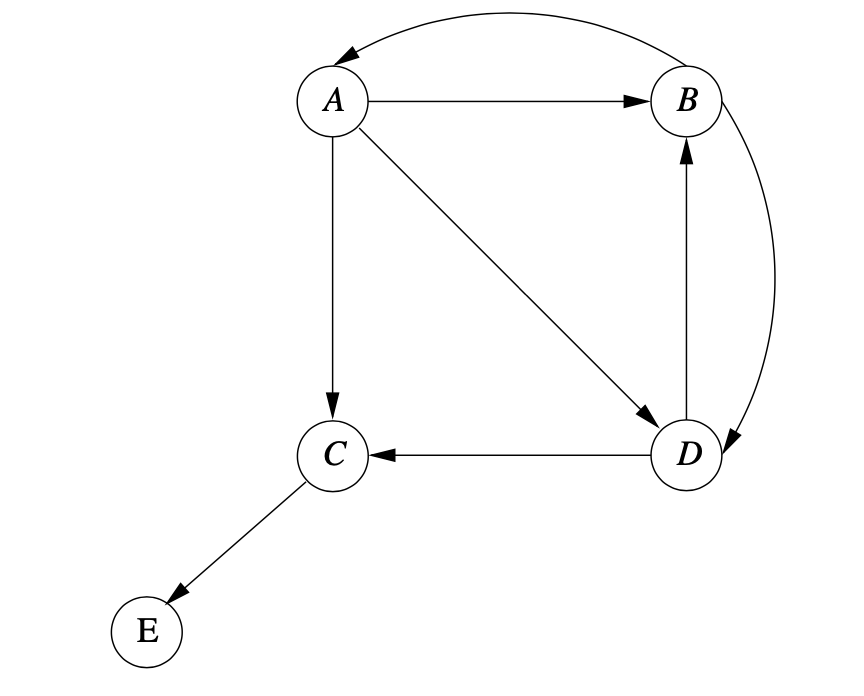
이미지 출처 : Mining of Massive Datasets - Figure 5.4

그림과 같은 상황을 가정해 봅시다.

여기서 E와 C 은 데드엔드가 됩니다. 이를 제거한 그래프 G 를 만듭니다.

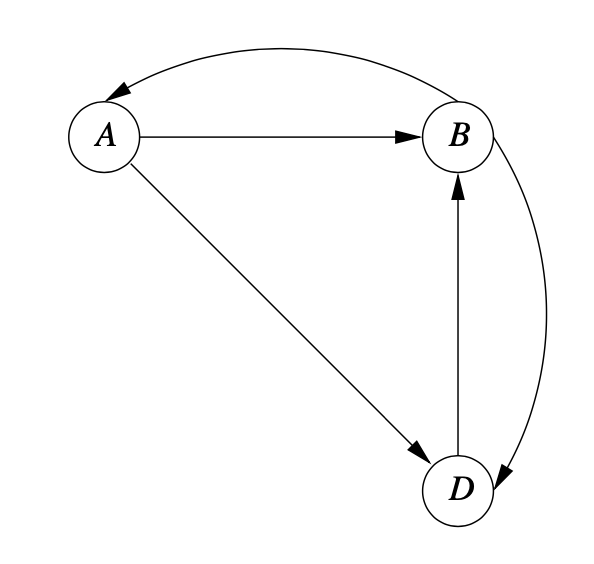
이미지 출처 : Mining of Massive Datasets - Figure 5.5

이 그래프에서 기존 방식대로 페이지랭크를 계산하면 $[\frac{2}{9} \frac{4}{9} \frac{3}{9}]^T$ 이 나옵니다. 이 페이지링크를 활용하여 C 의 페이지 랭크를 구합니다.

C의 값은 C로의 out link 가 있는 A 와 D 의 페이지랭크 값을 사용합니다.

A 로부터 A의 $\frac{1}{3}$, D 로부터 D의 $\frac{1}{2}$ 의 importance 를 받습니다.

그러므로 C 는 $(\frac{1}{2} \times \frac{2}{9}) + (\frac{1}{2} \times \frac{3}{9}) = \frac{13}{54}$ 가 됩니다.

E의 경우 C 에서 하나만 있으므로 동일한 값$\frac{13}{54}$을 갖게 됩니다.

이렇게 삭제된 순서의 반대로 순서로 노드를 구성하면서 Importance를 계산합니다.

데드엔드를 다루는 2번째 방식은 taxation으로, 스파이더 트랩(=Spider Traps) 을 다루는 방식과 동일하기 때문에 다음 파트에서 설명하겠습니다.

Spider Traps and Taxation

스파이더 트랩은 데드엔드는 아니지만 밖으로 나가는 링크가 없는 노드들의 집합입니다. 이러한 구조는 웹에 나타날 수 있고, 이는 페이지 랭크 계산이 스파이더 트랩에 해당하는 노드들 안에서만 일어나도록 만듭니다.

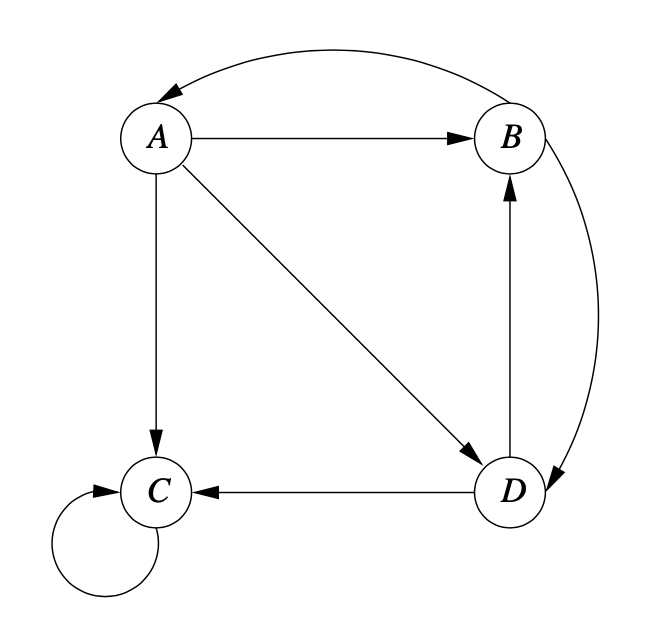
이미지 출처 : Mining of Massive Datasets - Figure 5.6

이 그림에서 스파이더 트랩은 C 하나 입니다. 일반적으로 스파이더 트랩은 많은 노드를 갖고 있습니다. 위 그림을 변환 행렬로 바꾸면

이와 같이 됩니다.

만약 기존 방식대로 페이지 랭크 계산을 반복한다면 다음과 같은 결과를 얻게 됩니다.

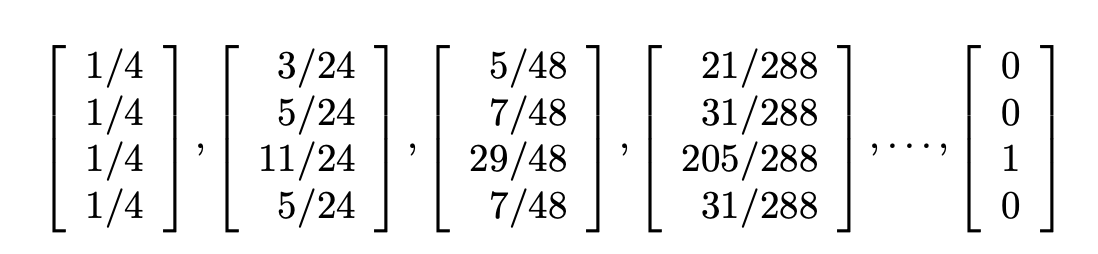
예상한대로 모든 페이지랭크가 C 에 있게 됩니다. 랜덤서퍼가 한번 빠지면 나올 수 없습니다.

이와 같은 상황을 피하기 위해 페이지 랭크 계산을 수정합니다.

서퍼가 트랩에 갇쳐도 다른 모든 페이지로 갈 수 있는 확률을 만들어 주는 것입니다. 이를 Taxation 라고 합니다.

각 랜덤 서퍼에 무작위 페이지로 가는 텔레포팅(=teleporting) 의 확률 $ 1-\beta$ 를 부여합니다.

이 확률은 다른 out-link 로 가는 확률보다는 작아야 합니다.

반복작업에서 페이지랭크의 새로운 백터 추정치인 v’ 를 계산합니다.

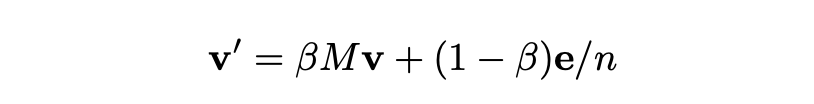
여기서 $\beta$ 는 상수이고 일반적으로 0.8~0.9 로 사용합니다. e 는 모든 요소가 1 로 된 벡터 입니다.

첫번째 항은 $\beta$ 를 갖고 랜덤 서퍼가 현재 페이지로부터의 아웃링크에 따라 가는 확률입니다.

두번째 항은 $(1-\beta)/n$ 값을 가진 컴포넌트들 각각의 벡터 이고, 이는 이어져 있지 않더라도 $(1-\beta)/n$ 의 확률을 가지고 다른 페이지로 이동하는 것을 나타냅니다.

이전 예시의 경우에서 에서 베타를 0.8로 두어 방정식을 다음과 같이 바꿀 수 있습니다.

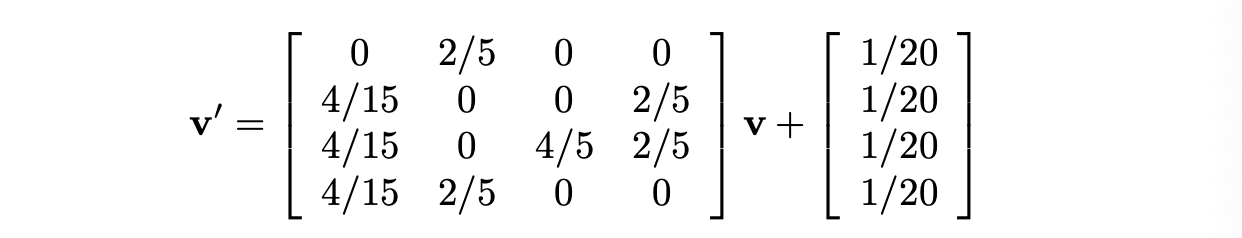
각 요소들에 $4/5$ 가 곱해진 M 과 베타를 통합합니다.

$(1-\beta)e/n$ 은 1/20 입니다. $(1-\beta = 1/5,n = 4)$

반복을 하다보면 다음처럼 됩니다.

이렇게 그래프 내 모든 노드로 갈 수 있는 작은 확률을 부여하여

데드엔드에서 다른 노드로 갈 수 있도록 하고,

스파이더 트랩에서 다른 노드로 갈 수 있도록 만들어 웹의 구조에 의해 발생하는 문제를 해결할 수 있습니다.

Compute PageRank

문제는 해결하였지만 식에 텔레포팅 항을 추가하게 된다면 연산의 어려움이 생깁니다.

이전 포스팅에서 언급한 것처럼,

웹 그래프는 대규모 데이터이지만, sparse 그래프여서 계산을 비교적 수월하게 할 수 있었습니다.

그러나 텔레포팅 항을 추가하게 되면 행렬 연산에서 모든 엔트리를 다 계산해야합니다.

\[\begin{bmatrix} 0 & \cdots&0.1 \\ 0.1 & \cdots&0 \\ 0 & \cdots &0 \\ \vdots & \cdots &\vdots \\ 0 & \cdots&0.2 \\ \end{bmatrix} \rightarrow \begin{bmatrix} 0.05 & \cdots&0.15 \\ 0.15 & \cdots&0.05 \\ 0.05 & \cdots &0.05 \\ \vdots & \cdots &\vdots \\ 0.05 & \cdots&0.25 \\ \end{bmatrix}\]

0이여서 빨리 넘길 수 있었던 항들을 다 계산해야하므로 계산량이 늘어나게 된것입니다.

이러한 문제를 처리하기 위해 약간의 트릭을 사용합니다.

실제 out-link 가 없는 항은 0으로 두고 계산하고, 계산한 결과에 텔러포팅 항을 더하여 수렴하는지만 비교 합니다.

텔레포팅 항이 상수이기 때문에 이러한 트릭이 가능합니다.

알고리즘을 보자면 다음과 같습니다.

이런식으로 행렬 연산에서 0을 만들어 계산량을 줄일 수 있습니다.

페이지랭크의 기본적인 내용에 관한 포스팅은 여기서 마칩니다.

추후 세부적인 사항들에 관해 정리하여 올릴 예정입니다.