PageRank - Random Surfer & Web Structure

해당 포스팅은 스탠포드의 Jure Leskovec 교수님의 강의 와 Mining of Massive Datasets(Jure Leskovec, Anand Rajaraman, Jeff Ullman) 책 을 참고하였습니다.

Random Surfer

한 사람이 있다고 가정해봅시다.

이 사람은 웹 서핑을 합니다. 현재 어떤 페이지에 머물러 있고 이 다음 시간, 스텝에는 머물러 있는 페이지에 연결된 링크 중 하나로 이동합니다.

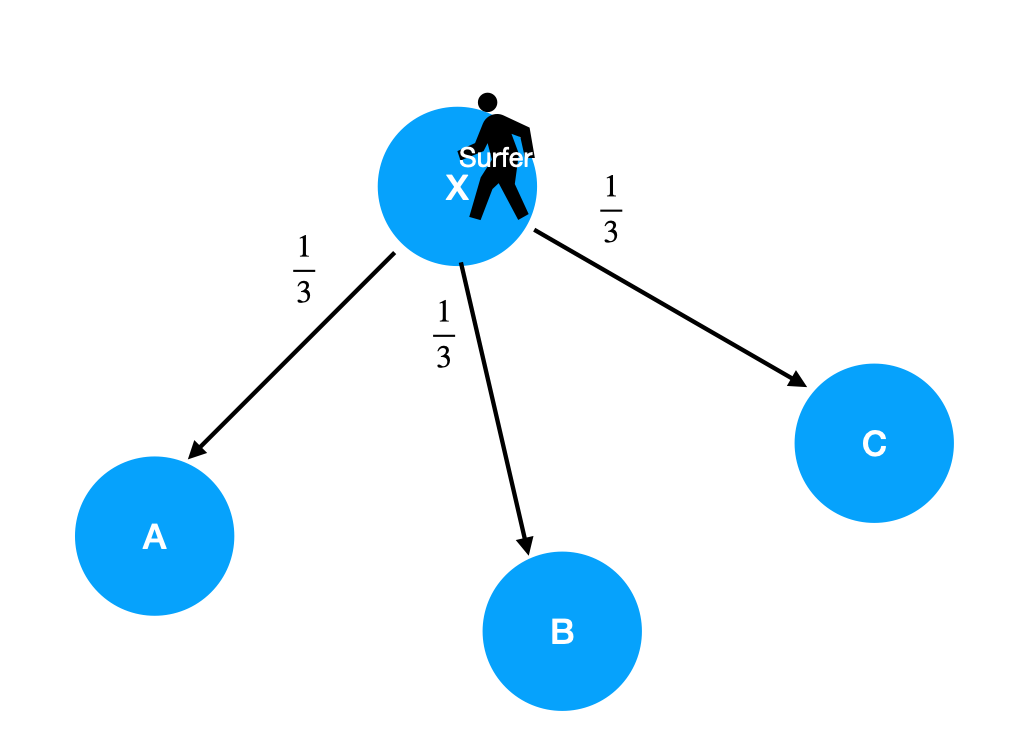
링크가 3개가 있고 각 링크를 따라 갈 확률은 동일하게 $\frac{1}{3}$ 이 됩니다.

랜덤 서퍼가 현재 페이지에서 다음 페이지로 갈 때 서퍼의 분포는 확률인접행렬을 곱한 값이 됩니다. $v_{n+1} = Mv_n$

이런 식으로 랜덤 서퍼가 계속해서 웹을 돌아다본다고 생각해봅시다.

서퍼가 있는 위치는 중요성을 나타내는 지표로 볼 수 있습니다. 직관적으로, 중요한 페이지의 경우, 많은 곳으로부터 연결이 되어 있습니다. 그래서 서퍼들이 그곳에 있을 확률이 비교적 높게 됩니다.

실제 우리의 패턴을 생각해봅시다. 웹을 사용할 때 우리는 주로 네이버나 페이스북 같은 유명하고 신뢰성있는 페이지에 머뭅니다. 여기선 무작위는 아니지만, 많은 사용자(서퍼)가 있다는 것이 페이지의 importance 를 나타내는 것으로 생각할 수 있습니다.

$p(t)$ 를 특정 시간 t에 서퍼가 어떤 페이지에 있는 확률을 나타내는 벡터라고 둡니다.

예를들어

$p(10) = \begin{bmatrix} 0.1\ 0.2\ \vdots \end{bmatrix}$

여기에서는 10번째 시간에서 첫번째 페이지에 있을 확률이 0.1이 되는 것입니다.

이렇게 $p(t)$ 를 표현하면 $p(t+1)$ 는 다음과 같이 구할 수 있습니다.

$p(t+1) = M \cdot p(t)$ 가 됩니다.

여기서 $p(t)$ 가 다음과 같은 상태에 도달하면

$p(t) = M \cdot p(t)$

$p(t)$ 는 Stationery distribution 이 됩니다.

이는 이전 포스팅에서 페이지랭크 벡터 $r = M \cdot r$ 와 동일합니다.

즉, 페이지랭크 벡터 r 은 랜덤서퍼(random walk)의 stationary distribution 이라고도 해석이 할 수 있습니다.

Markov process 이론에 따르면, 다음과 같은 조건을 갖어야만 $v= M\cdot v$ 인 stationary distribution를 갖을 수 있습니다.

1. 그래프가 Strongly Conntected Component 이다.
2. Dead ends 가 없다.

SCC(Strongly Conntected Component) 는 간략히 말하자면, 그래프 내의 어떤 노드든 다른 노드로 갈 수 있는 그래프입니다. 모두가 연결되었다는 의미는 아니고, SCC 내 다른 노드를 거쳐서든 어디든 도달할 수 있는 그래프입니다.

Dead ends 란 다른 노드로 향하는 링크(out-link)가 없는 노드를 말합니다.

그래프가 이런 두가지 조건을 만족하지 않는다면 랭크벡터 r 이 수렴하지 않고, 다르게 표현하자면 stationary distribution 를 구할 수 없습니다.

Structure of the Web

실제 웹은 SCC 가 아닙니다.

웹은 다음과 같은 구조를 갖고 있습니다.

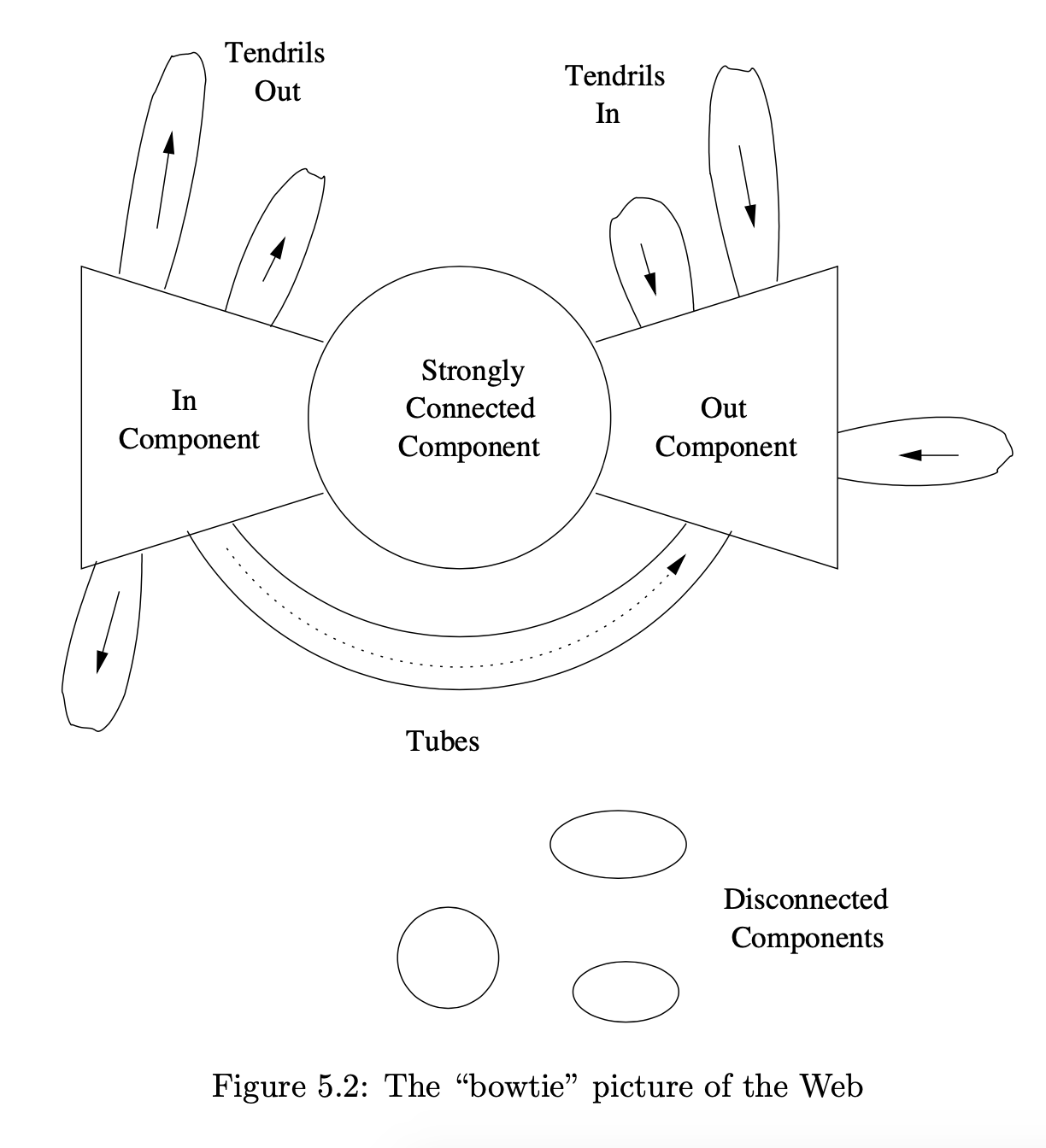
이미지 출처 : Mining of Massive Datasets - Figure 5.2

일부는 SCC 이지만 다른 컴포넌트들도 존재합니다.

• In-component : 링크를 따라 SCC 에 도달할 수 있는 페이지로 구성되지만, SCC가 해당 페이지에 도달할 수 없습니다.
• Out-component : SCC가 도달할 수 있지만 해당 페이지가 SCC 로 가지는 못합니다.
• Tendrils Out : In-component 이 도달할 수 있는 페이지들로 구성되어 있습니다.(in으로 갈 수는 없습니다.)
• Tendrils In : Out-component 로 도달할 수 있지만 out에서 갈 수는 없습니다.
• Tubes : In-component 가 도달할 수 있고 Out-componet 로 갈 수 있습니다. 그러나 SCC 에 도달하거나 SCC 에서 올 수 없습니다.
• Isolated components : 위의 컴포넡트들로 갈 수도 없고 거기서 오지도 않습니다.

웹의 이러한 부분들은 Markov process 로 수렴하기 위해 필요한 가정들을 위반합니다.

랜덤서퍼가 Out-component 인 페이지로 들어가게 되면, 이후 다시 나올 수 없게 됩니다. 이러면 SCC나 In-component 에서 시작한 서퍼는 Random walk를 하다가 결국엔 Out-component 나 Tendrils Out 으로 가게됩니다. 때문에 기존 방식대로 수행을 한다면 SCC, In-component 의 페이지 importance 는 0 이 됩니다.

위와 같이 기존 방식에서 발생할 수 있는 문제는 2가지로 정리할 수 있습니다.

Out link 가 없는 노드, 데드엔드(=Dead Ends) 가 있는 경우, 서퍼는 그 노드에서 다음 스텝을 진행할 수 없게 됩니다.

다른 컴포넌트로 갈 수 없는 구조, 스파이더 트랩(Spider traps) 이 있는 경우입니다.

다음 포스팅에서 이 문제들에 대해 다루겠습니다.