PageRank - Stochastic adjacency matrix

해당 포스팅은 스탠포드의 Jure Leskovec 교수님의 강의 와 Mining of Massive Datasets(Jure Leskovec, Anand Rajaraman, Jeff Ullman) 책 을 참고하였습니다.

페이지 랭크를 행렬로 변환하기에 앞서

행렬과 그래프관련 기초적인 지식을 간단히 짚어보겠습니다.

그래프의 표현 방식

그래프 형태의 구조를 표현하는 방식은 2가지가 있습니다.

Ajacency list 와 Ajacency matrix 입니다.

인접리스트 (Ajacency list)

Ajacency list 는 하나의 노드 당 연결된 linked list 로 그래프를 표현하는 방식입니다.

모든 노드의 수 N 만큼의 linked list 가 있습니다.

엣지의 수에 따라 데이터의 크기가 커집니다. 그래서 엣지가 적은 Sparse Graph 에 주로 사용합니다.

이 그래프는

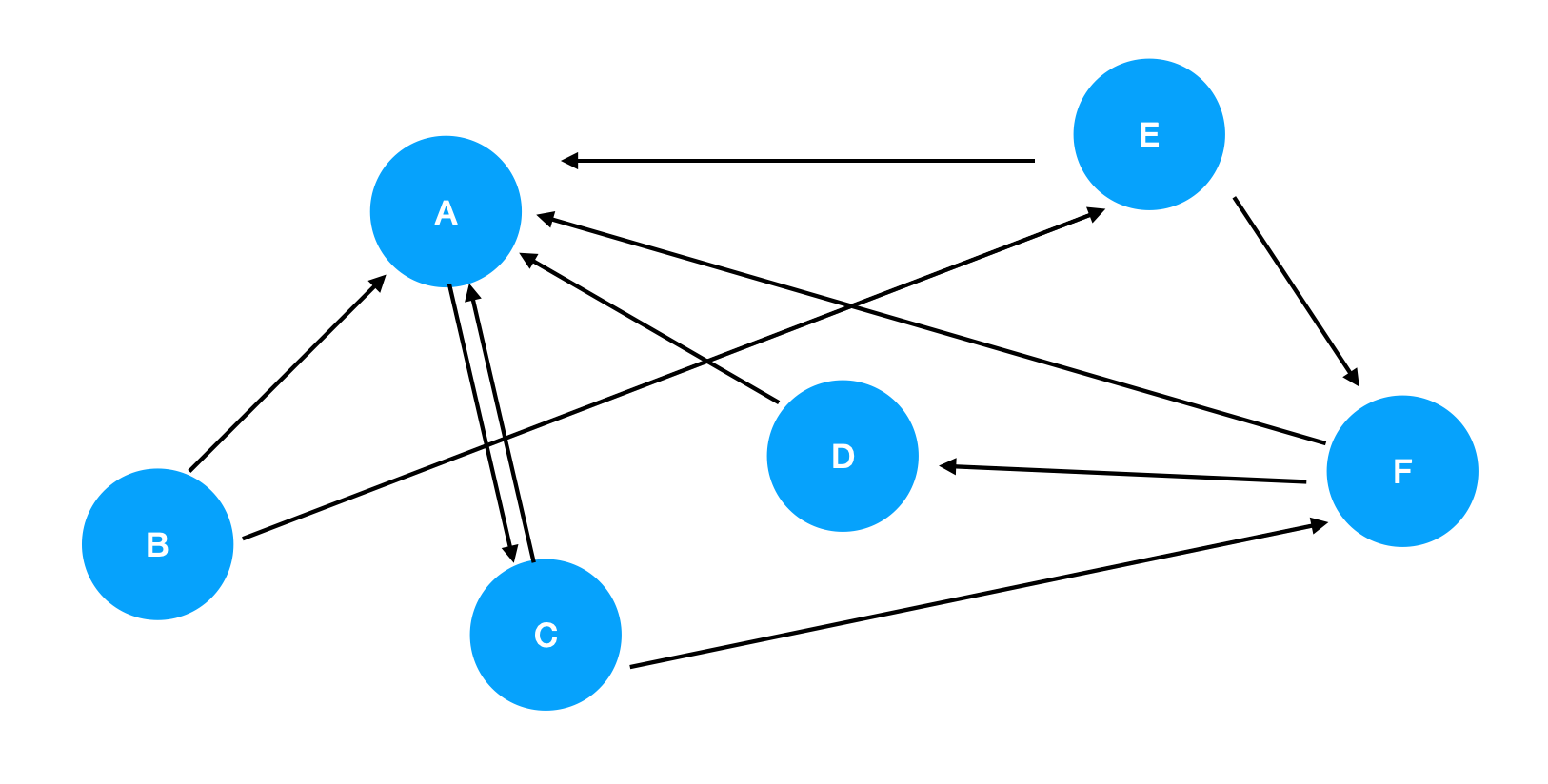
다음과 같이 표현될 수 있습니다.

A $\rightarrow$ C

B $\rightarrow$ A - E

C $\rightarrow$ A - F

D $\rightarrow$ A

E $\rightarrow$ A - F

F $\rightarrow$ A - D

인접 행렬 (Ajacency Matrix)

Ajacency Matrix 는 $N\times N$ 크기의 행렬 M 을 사용하여 그래프를 표현합니다.

$i$ 번째 노드의 엣지가 $ j$ 번째 노드를 연결한다면 $M_{ij} = 1$ 로 두어 표현합니다.

위 그림을 Ajacency Matrix 로 표현하면 다음과 같습니다.

\[M= \begin{bmatrix} 0 & 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 & 0 & 0 \\ \end{bmatrix}\]

그래프 구조를 다룰 때 대부분의 경우 이 방식을 사용합니다.

행렬로 데이터를 표현하면 선형대수의 여러 기술들을 사용할 수 있으며, 병렬 처리하기 적합하는 등의 여러 이점이 있습니다.

확률 인접 행렬 (Stochastic adjacency matrix)

Stochastic adjacency matrix 는 노드 i 에서 j 로 가는 out-link 의 확률을 행렬로 표현한 것입니다.

노드 i 의 전체 out-link 의 수를 $d_i$ 라 하면,

특정 노드 j 로 가는 out-link 가 있을 때 이 확률은 $\frac{1}{d_i}$ 이되고,

행렬 $M$ 은 다음 식으로 표현할 수 있습니다.

$M_{ji} = \begin{cases} \frac{1}{d_i}, & \mbox{if } i \rightarrow j
0, & \mbox{else} \end{cases} $

$M$ 의 열(column)은 확률을 나타내므로, 총합이 1 이 됩니다.

그래서 $M$ 을 column stochastic matrix 이라고도 합니다.

이제 이 행렬을 사용하여 각 노드의 Importance 를 표현할 수 있습니다.

랭크 벡터 (Rank Vector)

랭크 벡터란 각 페이지 항목에 대한 벡터입니다.

랭크 벡터 $r_i$ 는 페이지(노드) i 의 중요도를 의미합니다.

이전 포스팅에서 설정하였듯이 모든 페이지의 중요도 합은 1 이고

$\Sigma_i r_i = 1$ 로 표현할 수 있습니다.

이제 랭크벡터 $r$ 과 확률인접행렬(=Stochastic adjacency matrix) $M$을 사용하여 이전의 flow equation을 표현할 수 있습니다.

$r = M\cdot r $

위 식의 의미에 대해 살펴보겠습니다.

$M$ 의 i 행은 다른 노드들에서 노드 i 로 갈 수 있는 확률을 나타냅니다.

\[M= \begin{bmatrix} 0 & \frac{1}{2} & \frac{1}{2} & 1 &\frac{1}{2} & \frac{1}{2} \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{1}{2} \\ 0 & \frac{1}{2} & 0 & 0 & 0 & 0 \\ 0 & 0 & \frac{1}{2} & 0 & \frac{1}{2} & 0 \\ \end{bmatrix} , r = \begin{bmatrix} \frac{1}{6} \\ \frac{1}{6} \\ \frac{1}{6} \\ \frac{1}{6} \\ \frac{1}{6} \\ \frac{1}{6} \\ \end{bmatrix}\]

여기서 첫번째 행(A)을 보자면,

B 가 A 로 갈 확률 $\frac{1}{2}$ , D가 A 로 갈 확률 $1$ 을 나타냅니다.

그리고 r 은 각 페이지의 importance 점수를 나타냅니다. (일반적으로 $\frac{1}{n}$ 으로 초기화 합니다.)

A의 행과 r 을 곱한다면, 각 페이지로 부터 importance 를 받은 값이 나오게 됩니다.

확률인접행렬의 고유벡터 (eigenvector of the stochastic adjacency matrix)

flow equation 을 랭크벡터 r 과 확률인접행렬 M 을 사용하여 변환한 식을 다시 살펴봅시다.

$r = Mr$

이 식의 형태를 잘보면 뭔가 떠오를 수 있습니다.

선형대수에서 행렬 A의 고유값을 구하는 공식은 다음과 같이 표현하였습니다.

$Ax = \lambda x$

여기서 고유값 $\lambda$ 가 1인 경우 $Ax = x$ 가 됩니다. 그리고 이 형태는 위의 flow equation 의 변환식과 동일한 형태를 갖습니다.

그럼 페이지랭크를 다음과 같이 해석할 수 있습니다.

’ 페이지랭크 벡터 r은 확률 인접 행렬 M 의 고유값이 1일 때의 고유벡터이다.’

앞서 말한 것처럼 행렬 M은 확률적(stochastic) 입니다. 각 column에서 성분의 합이 1이됩니다. 이런 행렬의 고유값 중 최대값은 1이고 이를 principal eigenvalue 라고 합니다. (증명) principal eigenvalue 의 고유벡터, principal eigenvector 는 페이지의 importance 를 나타냅니다.

주어진 행렬 고유값이 정확하게 1인 경우는 매우 드뭅니다. 바로 계산할 수 없기 때문에 power iteration method 를 사용하여 고유벡터를 추정할 수 있습니다.

power iteration method는 고유값 중 가장 큰 값(principal eigenvalue) 에 해당하는 고유벡터만 구할 수 있습니다.

+ inverse iteration : 고유값 중 가장 작은 값에 해당하는 고유벡터를 구하는데 사용

Power Iteration Method

이 방식은 principal eigenvector 를 추정하기 위해 사용합니다.

초기 벡터 $r_0$ 는 모두 같도록 설정해 줍니다.

$r_0 = \begin{bmatrix} \frac{1}{n}\ \vdots \ \frac{1}{n} \end{bmatrix} $

그리고 행렬 M 을 계속해서 곱해줍니다.

$r = M^kr$ 행렬의 곱한 결과가 변화가 거의 없을정도까지, 수렴할 때 까지 곱합니다.

\[r = \begin{bmatrix} \frac{1}{12}\\ \vdots \\ \frac{1}{12} \end{bmatrix} , \begin{bmatrix} \frac{4}{11}\\ \vdots \\ \frac{17}{21} \end{bmatrix} , \cdots , \begin{bmatrix} \frac{1}{4}\\ \vdots \\ \frac{2}{3} \end{bmatrix}\]

실제 웹에서는 50~75 회 정도 반복하면 어느정도 수렴된다고 합니다.

여기서 행렬의 곱이 수렴을 하지 않는 경우가 생길 수 있습니다. 이는 페이지랭크의 두가지 문제 상황과 관련이 있는데 다음 포스팅에서 다뤄보겠습니다.

페이지랭크 벡터를 수렴시키려면 수십번의 반복 연산을 수행해야합니다. 이렇게 계산하는 것이 합리적인것이가 라고 생각할 수 있습니다.

앞선 포스팅에서는 연립방정식을 그대로 푸는 방식(Gaussian Elimination)으로 접근을 해보았습니다. 이 방식은 계산량이 $O(n^3)$ 이 걸리는 방식입니다.

Power iteration 은 행렬의 곱, 한번에 $n^2$ 의 계산을 수행합니다. $n^2$ 의 연산을 많이 반복하여 수행하지만 그래도 결국엔 $O(n^2)$ 입니다. 웹 같은 경우는 데이터의 수가 매우 많기 때문에, 이런 degree의 차이는 엄청난 차이가 됩니다.

또한 실제 웹 같은 경우 그래프가 sparse (링크가 적음, 0이 많은 행렬) 합니다. 그래서 연산 속도를 더 높일 수 있습니다. 웹은 평균적으로 페이지 당 10개의 링크가 존재한다고 합니다. (nonzero entry가 10개)

이러한 연산 상의 이점들로 인해 페이지랭크에서는 Power iteration method를 사용합니다.

다음 포스팅에서는 페이지랭크를 랜덤서퍼(random surfer) 의 관점에서 보고, 실제 웹의 구조와 거기서 파생되는 문제들에 대해 다뤄보겠습니다.