PageRank - Importance

해당 포스팅은 스탠포드의 Jure Leskovec 교수님의 강의 와 Mining of Massive Datasets(Jure Leskovec, Anand Rajaraman, Jeff Ullman) 책 을 참고하였습니다.

Basic concept

페이지랭크의 기본 컨셉은

‘링크가 많을수록 더 중요한 페이지이다.’ 입니다.

링크는 방향그래프이므로 in, out 두가지 종류가 있는데,

일반적으로 in-comming link 를 기준으로 합니다.

Out-going link 는 페이지 생성자가 임의로 만들어 낼 수 있기 때문에 중요도를 나타내는 척도로 사용하기가 어렵습니다.

우선 in-comming link 기준으로만 페이지의 랭크를 매겨 봅시다.

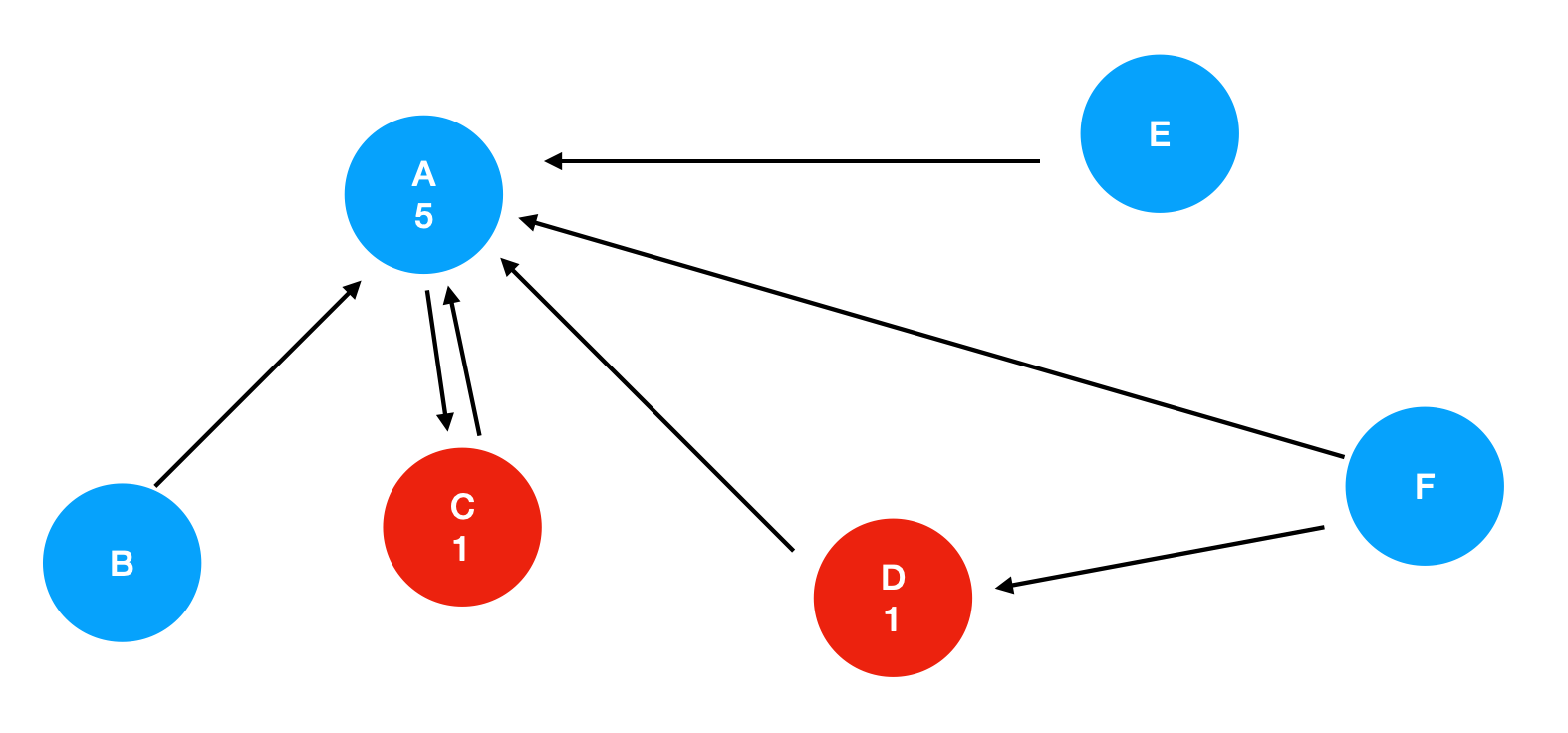
여기서 C와 D는 in-comming link 수가 동일하기 때문에 같은 점수를 갖습니다.

그러나 C와 연결된 페이지는, D와 연결된 페이지 보다 더 높은 중요도를 갖습니다. 이렇게 상황이 다른데 동일한 점수로 취급하는 것은 합리적이지 않습니다.

때문에 ‘중요한 페이지의 링크는 다른 링크보다 더 높은 중요도를 갖는다’ 라는 개념을 도입하게 됩니다.

그림으로 보면 다음과 같습니다.

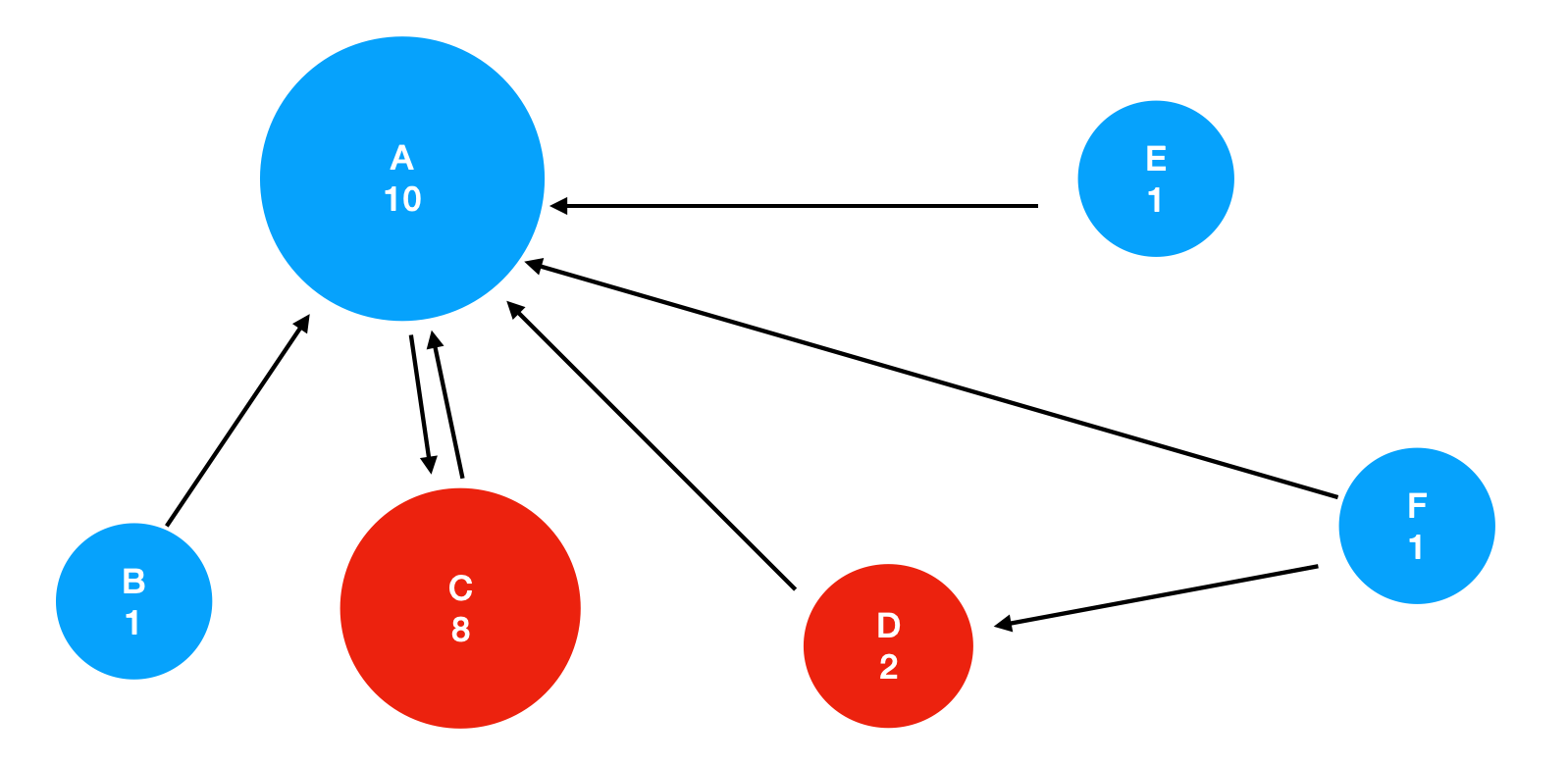
(그림의 중요도 값은 이해를 돕기 위해 임의로 설정한 값입니다.)

C,D 는 동일한 링크를 갖지만, C와 연결된 노드(A)는 D와 연결된 노드(F)보다 더 높은 점수를 갖습니다. 그래서 더 높은 점수를 갖게 됩니다.

이런 두가지 개념

• 링크가 많을수록 더 중요한 페이지이다.
• 중요한 페이지의 링크는 다른 링크보다 더 높은 중요도를 갖는다

을 사용하여 페이지랭크 공식을 만들 수 있습니다.

Node Importance Equation

위의 컨셉을 공식화하기 위해 재귀를 사용해야합니다.

단순히 링크 수만 세는 경우는 상관없지만,

중요한 노드와 연결된 한 노드는 기존 보다 높은 중요도를 갖고

또 이 노드와 연결된 노드도 기존 보다 높은 중요도를 갖게됩니다. 이렇게 propagate의 형태를 띄기 때문에 재귀적으로 수행을 해야합니다.

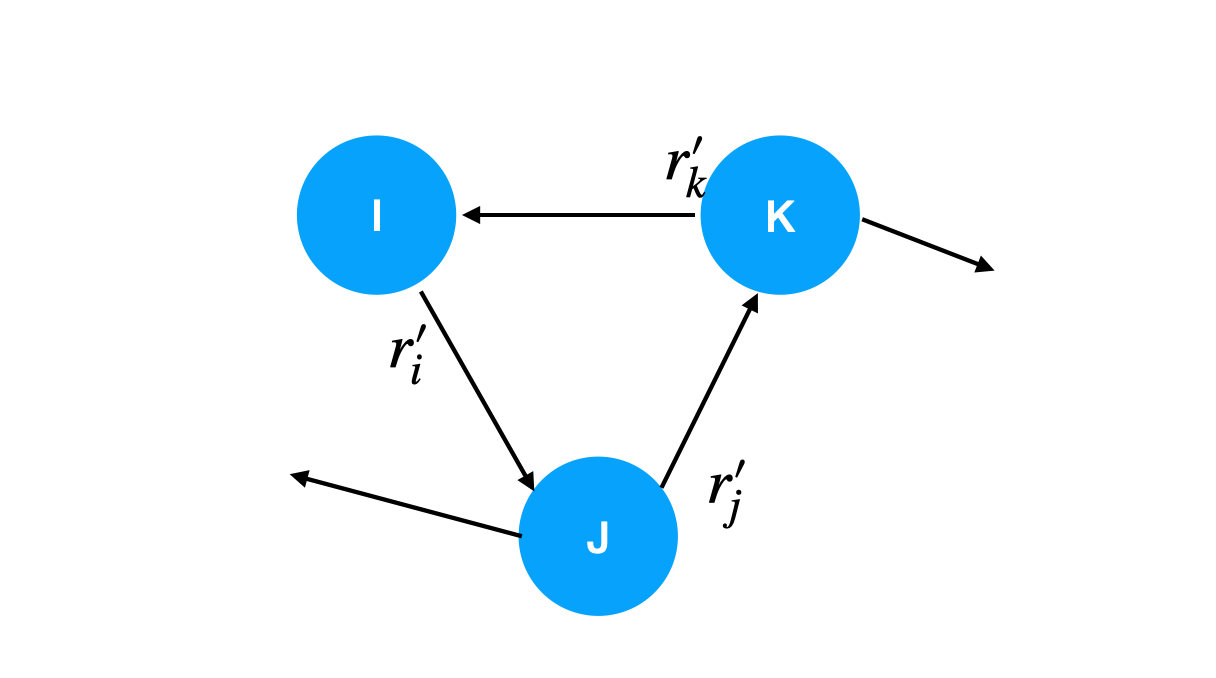
우선 한 노드에 대해서 봅시다.

노드 $j$ 가 있고, $j$ 의 중요도를 $r_j$ 로 표현합니다.

노드 $j$ 에서 다른 노드로 가는(out-going) 링크의 수를 n 이라고 하면

그 링크와 연결된 다른 노드들은 각각 $\frac{r_j}{n}$ 의 중요도를 더하면 됩니다.

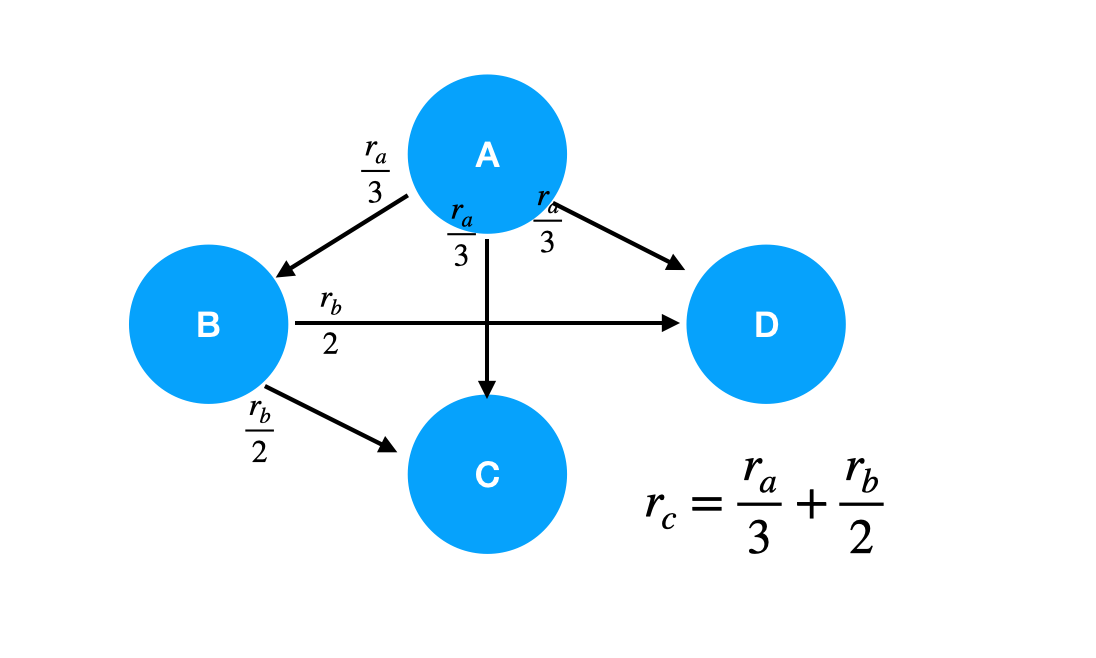
노드의 중요도는 다른 노드들로부터 받은 중요도의 합 이므로 다음과 같이 표현할 수 있습니다.

\[r_i = \Sigma_{i\rightarrow j} \frac{r_i}{d_i}\]

$(d_i$ 는 $i$ 의 out-degree)

이런식으로 각 노드들에 대한 중요도 방정식을 생성할 수 있습니다.

노드의 중요도가 propagate 되는 특성을 일컬어 flow 라 표현하고,

이 방정식을 flow equation 이라고 표현합니다.

이 방정식들을 풀 수 있는지 생각을 해봅시다.

n개의 노드가 있다면, 각 노드당 하나의 식이 도출됩니다.

그래서 n 개의 식이 생기고, 미지수는 노드의 수 n 개가 있습니다.

이 식에서는 상수가 없으므로 유일해(unique solution) 를 구할 수 없습니다.

여기서 새로운 식을 하나 추가해, 유일해를 구하도록 조정할 수 있습니다.

importance 의 총합에 대한 식을 추가해 줍니다.

일반적으로 총합을 1로 둡니다.

\[\Sigma_i r_i = 1\]

이렇게 식을 추가해 중요도에 대한 연립방정식의 해를 구할 수 있습니다.

연립방정식을 그대로 풀 수 있지만 (노드가 많으면 현실적으로 불가능합니다.)

컴퓨터에서는 행렬으로 변환 사용하여 푸는 것이 효율적입니다.

다음 포스팅에서는 이 flow equation을 행렬을 사용해 표현해보고, 어떤 의미를 갖는지에 대해 정리해보겠습니다.